Sorting faster than O(n log n).
Intro
Find the most frequent number in the array A with a size of N containing positive integers with a max size of M.
N = 9
M = 2^5
A = [1, 10, 9, 8, 10, 2, 5, 1, 6]
There are many ways to solve this. One of the more efficient ways is to use a dictionary or hash map to build a key: value mapping.
What if we needed to sort the array?
Can you sort faster than O(n log n) in certain circumstances? What if we have certain guarantees about the amount of numbers we have to consider and their size?
Counting sort
N = 9
M = 2^5
A = [2, 6, 14, 31, 14, 4, 2, 19, 14]
B = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
Count
We are going to use the array B to track the frequency of numbers in array A. Array B will be initialised to zero. It will have M elements.
The index of each element in the array B will represent the numeric value in array A.
For example. Zero is not an element in the array A so we expect the first element in array B to remain with a count of zero. We expect the first element in the array A to have a count of two in the array B.
This corresponds to the third element in array B. See the figure below. The blue numbers are the index of the array B.

You would expect to see the index of 13 in the array B have a value of 3.
Sort
We now have an array B that looks like the below.
B = [0, 0, 2, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 3, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0]
We use this count to construct a new array A’ that is sorted. We do this by iterating through B and adding the index we are at in B to A.
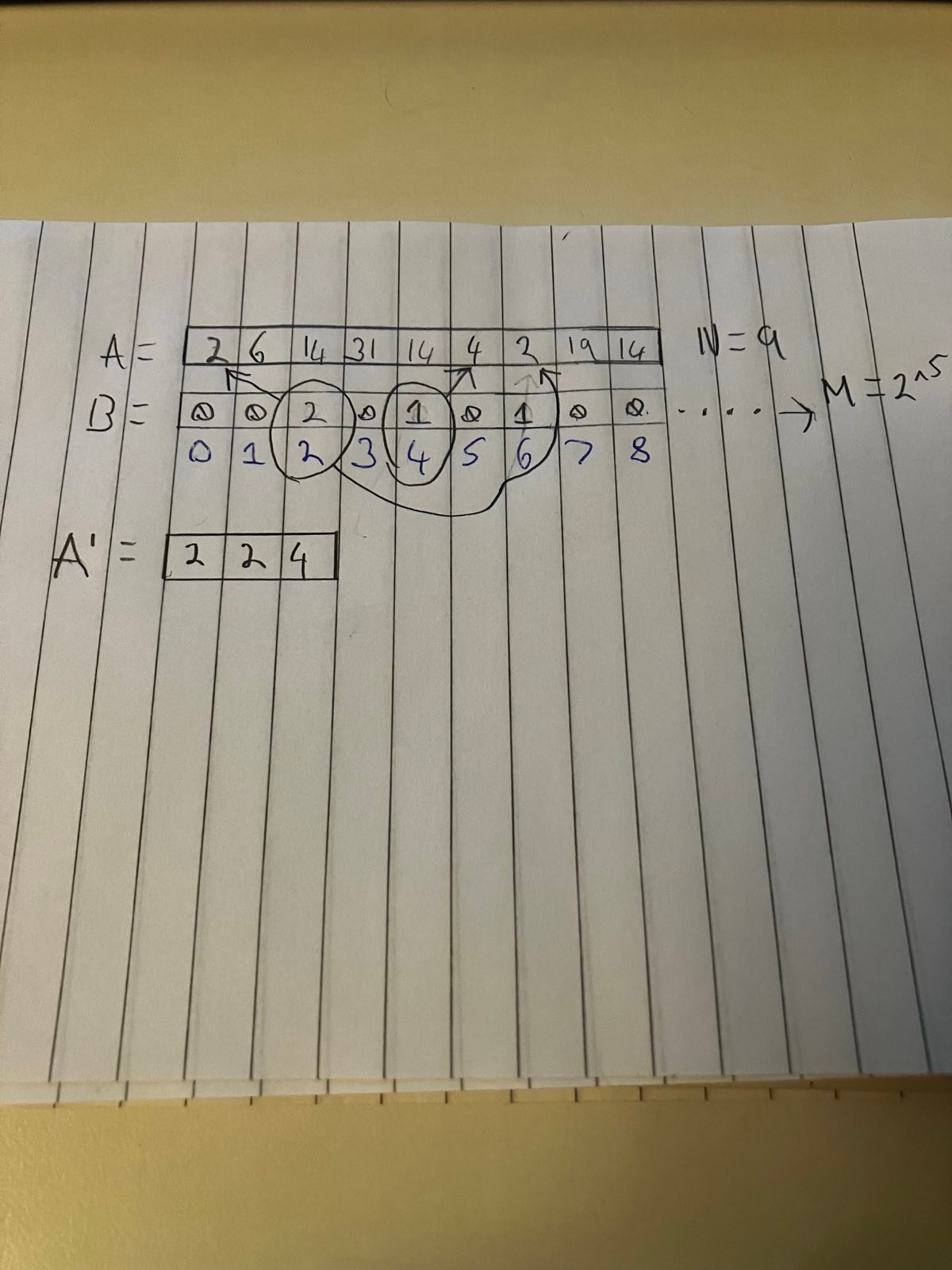
Remember the index in B corresponds to the element value in A. The element value in B corresponds to the number of times that number appears in A.
A’ = [2, 2, 4, 6, 14, 14, 14, 19, 31]
This results in a sort of O(N + M) where N is the total number of elements in the array and M is the size of the largest element.
Remember we are doing an O(n) iteration of array A. O(1) update to the array B because we know the index that we want to increment.
Outro
This is why understanding order of growth and exponents is important. It will greatly improve your ability to solve problems. An approximate solution is better than a wild guess.
This is how I feel about my handwriting.

In the episode Bart is sick and the note provided to the school looks like it was written by a child. It was written by Homer.
Radix sort builds upon the premises of Counting sort so I have included it in the references below.